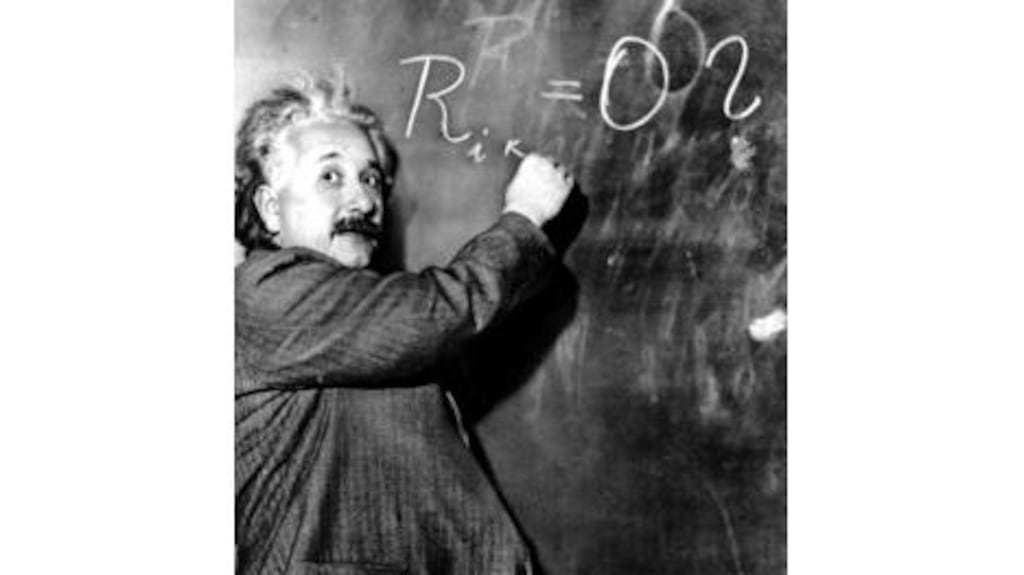The connections between mathematics and physics are manifold, and each enriches the other. But the relationship between the disciplines fluctuates between intimate harmony and cool indifference.
Numerous examples show how mathematics, developed for its inherent interest in beauty, later played a central role in physical theory. A well-known case is the multidimensional geometry formulated by Bernhard Riemann in the mid 19th century, which was exactly what Albert Einstein needed 50 years later for his relativity theory.
Einstein was initially dismissive of mathematics. When his professor, Hermann Minkowski, established a geometric basis for the space-time of special relativity, Einstein described it pejoratively as “superfluous learnedness”. Within a few years, realising the error of his view, Einstein pleaded with his friend Marcel Grossmann to help him master the advanced theory of tensor calculus, which was of key importance for his general theory of relativity.
Mathematics and physics thrive when they enrich each other. Newton, Euler, Gauss and Poincaré all produced wonderful ideas in both theoretical physics and pure mathematics. In 1939 physicist Paul Dirac spoke about a merger of the two subjects but, for the following 50 years, there was little symbiosis and the two fields developed independently, with little or no cross-fertilisation.
Are Loughmore-Castleiney and Slaughtneil what all GAA clubs should strive to be?
Chasing the Light review: This agreeable Irish documentary is all peace and healing. Then something disturbing happens
Your work questions answered: Can bonuses be deducted pro-rata during a maternity leave?
John Montague: A Poet’s Life by Adrian Frazier: ‘ruthless intimacy’
Physicists used established mathematical methods, rarely producing new ideas of interest to mathematicians. Most leading mathematicians showed no interest in physics but focused on the foundations of mathematics and fields of increasing abstraction.
There were some notable exceptions: John von Neumann, a brilliant Hungarian-American who excelled in both physics and mathematics, formulated a solid system of mathematical axioms for set theory and also established a sound framework for quantum mechanics. In contrast, Richard Feynman managed to produce creative advances in physics with minimal mathematics – he was unconcerned with mathematical rigour.
From the 1960s on, it became increasingly clear that progress in theoretical physics required – and stimulated – new mathematics. The physics of black holes raised some knotty mathematical problems. The role of symmetry in physics was best described using the mathematical field of group theory. Clearly, mathematicians and physicists could benefit by learning about each other’s work.
When mathematician Hermann Weyl and physicist Eugene Wigner introduced group theory into quantum mechanics in the early 1920s, Einstein dismissed it as unimportant; had he forgotten his earlier enlightenment?
Group theory is now indispensable in theoretical physics. It has revealed the existence of several unknown subatomic particles. The size of the largest simple finite group, dubbed the Monster Group, has 54 digits. Theoretical physicist and mathematician Freeman Dyson remarked that “sometime in the 21st century physicists will stumble upon the monster group, built in some unsuspected way into the structure of the universe”. We await such a development.
The foundations of mathematics were severely shaken in 1931 when Kurt Gödel proved the inherent incompleteness of the underlying axiom system. While most mathematicians carried on regardless, logicians continued to search for damage-limitation strategies.
Physics is also in crisis: the standard model, based on quantum mechanics and special relativity, is a superb achievement, yielding results of great precision, but it omits the crucial field of gravity, so it cannot explain the very early evolution of the universe. A unified theory is needed and the search for it is ongoing.
Peter Lynch is emeritus professor at the school of mathematics and statistics, University College Dublin. He blogs at thatsmaths.com